Common States of Stress

There are many ways that stress and strain can be embodied in a material. We'll first want to introduce common (sometimes called simple) states of stress that are easily defined. In addition to stress due to tension explored on the previous page Section 11.3, there are a number of other common states of stress. This page illustrates them (including tension again for completeness). These are especially important in materials science because we need to quantify mechanical properties. Complex states of stress would yield complex measurements which are difficult to interpret. So we often put materials in well-controlled, simple states of stress when performing standardized characterization of their mechanical properties.

Please either read the text below or watch the video at the end of page and then answer the question in Exercise 11.6.1.

The simple types of stress are:

  • Uniaxial (simple) tension
  • Uniaxial (simple) compression
  • Pure shear

Each of these are illustrated below with their formulas for stress and strain.

There are also some more complicated types of stress:

  • Torsion (another type of shear)
  • Biaxial tension/compression
  • Hydrostatic tension/compression

These last three are illustrated below, but as they are more complex states, we'll illustrate them without formulas.

Uniaxial (simple) tension

This was covered on the previous page but is included here for completeness.

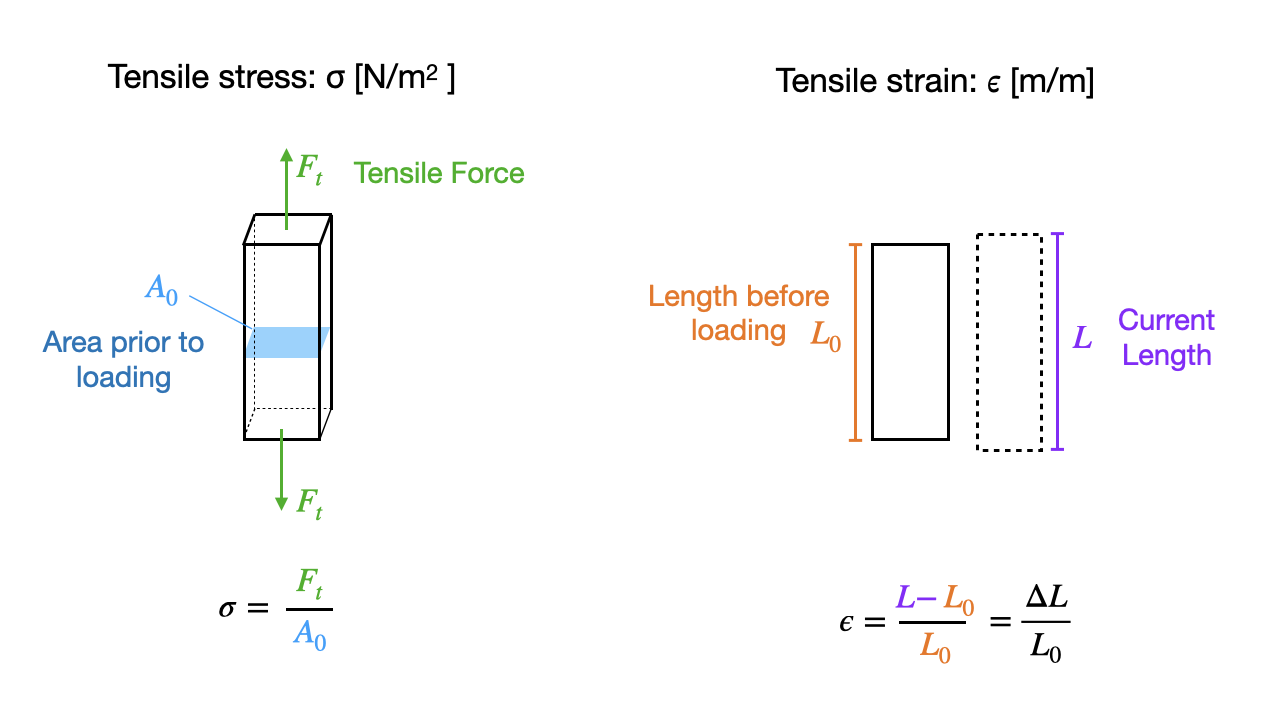
Tensile stress and tensile strain defined and illustrated.

Figure 11.6.1 Tensile stress and tensile strain defined and illustrated.

Uniaxial (simple) compression

Uniaxial compression is essentially the opposite of tension. It is very common in buildings (e.g., a column is under uniaxial compression).

Compressive stress and strain defined and illustrated.

Figure 11.6.2 Compressive stress and strain defined and illustrated.

Pure Shear Stress

Shear stress occurs when two parts of a material are pushed in opposite directions.

Shear stress defined and illustrated.

Figure 11.6.3 Shear stress defined and illustrated.

Torsion

Torsion is a type stress applied in a twisting motion/torque (Figure 11.6.4). This type of loading will essential yield local shears - as demonstrated in the diagram in Figure 11.6.5

A bar under torsion ([source](https://en.wikipedia.org/wiki/Torsion_(mechanics)#/media/File:Twisted_bar.png))

Figure 11.6.4 A bar under torsion (source)

A diagram of a cylindrical shell with vertical lines on the outside (imagine a cylinder with toothpicks lining the outside). The lines will *shear* past each other due to torsion.

Figure 11.6.5 A diagram of a cylindrical shell with vertical lines on the outside (imagine a cylinder with toothpicks lining the outside). The lines will shear past each other due to torsion.

Hydrostatic stress

Hydrostatic stress is generally the result of a fluid pressing on an object equally in all directions. It is often also just called pressure.

Hydrostatic tension and compression.

Figure 11.6.6 Hydrostatic tension and compression.

Biaxial Tension/Compression

Biaxial stress is stress applied to a planar (or approximately planar) material in two directions at once (bi = two and axial = related to axes). A common example of a material in approximately biaxial tension is the surface of a balloon (or any other pressurized container).

Biaxial tension diagram. The material of an inflated balloon is under biaxial tension.

Figure 11.6.7 Biaxial tension diagram. The material of an inflated balloon is under biaxial tension.

Why Does the Type of Stress/Strain Matter?

Materials respond differently to different types of stress. So, for any given application, we need to account for the types of stress the material will undergo and select/design materials appropriately. Let's consider a personal one for my past in Exercise 11.6.1 below!

The Ice Cube Observatory (left), with optical modules and bore holes (right). ([source](https://en.wikipedia.org/wiki/IceCube_Neutrino_Observatory))

Figure 11.6.8 The Ice Cube Observatory (left), with optical modules and bore holes (right). (source)

Exercise 11.6.1: Hanging on a Wire
Not Currently Assigned

When I (Jon Emery) was in college, I worked at UW-Madison's Physical Science Laboratory (as a janitor) during the summers. This was a great experience, I saw some of my first big machines, including the UW-Madison's (now-defunct) synchrotron - an X-ray source used to study materials. I ended up doing my doctoral thesis using synchrotrons around the world!

While I was there, the Physical Science Lab was contracted to work on a project called Ice Cube, which is a gigantic neutrino detector in Antarctica (Figure 11.6.8). Simply, the way the it works is that, sometimes, when neutrinos hit very pure ice, produce a flash of light. The Ice Cube project embedded thousands of optical sensors in this ice, positioned along long steel cables in bore holes. They've had great success in using this big machine to study neutrinos.

  1. However, when first testing the cables, they frequently broke under what was expected (by the engineering firm) to be normal operating conditions. What states of stress might you think are important in these cables, and can you guess what the engineering firm might have done wrong?

    This is just a bit of a thought experiment - no need to "get this right", just think about what states of stress might exist.