Elastic Properties
There are a number of measurable material properties associated with elastic deformation. As we saw with the model of stress-strain, NetLogo model 11.3.1, during elastic deformation bonds stretch but don't break. As a refresher, this is visualized in Figure 11.4.1 below. Elastic properties refer to the region of the stress-strain curve that is approximately linear.

Figure 11.4.1 An animation produced with NetLogo model 11.3.1 of elastic deformation.
Modulus of Elasticity (Young's Modulus)
As we saw, the stress-strain curve produced by NetLogo model 11.3.1 starts out approximately linear. This is true for a large-class of real materials including:
- Most metals
- Nearly all ceramics
- Some polymers
How difficult it is to strain a material in this linear range is known as the modulus of elasticity or Young's Modulus (named for Thomas Young even though others had used the concept before him). It is equal to the slope of the stress-strain curve in the linear region, as shown below in Figure 11.4.2, and defined as:
In the elastic region, displacement (strain) is then proportional to applied stress: $\sigma=E\epsilon$. This is just a mathematical restatement of the fact that the stress-strain curve is linear in this region.
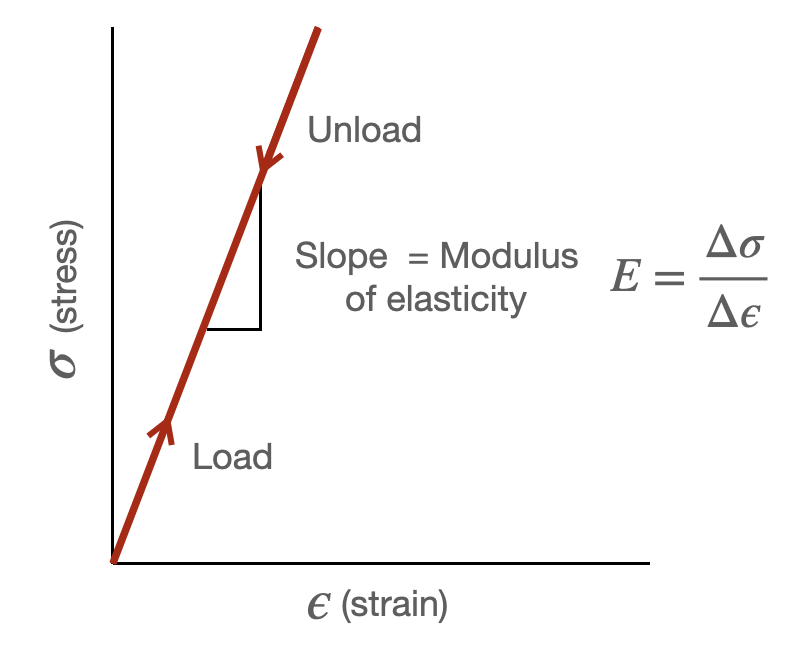
Figure 11.4.2 Illustration of modulus of elasticity
The modulus of elasticity is directly related to the interatomic potential as discussed in the solution to Question 11.3.1.4. $E$ is the slope of the interatomic force vs displacement (or strain) graph $E=\frac{dF}{d\epsilon}$. We also know that the force is proportional to the slope of the interatomic potential $F=\frac{dU}{d\epsilon}$. So:
$$E=\frac{dF}{d\epsilon}=\frac{d^2U}{d\epsilon^2}$$
That is, the modulus of elasticity is directly related to the curvature of the interatomic potential. This makes sense if we think of the linear elastic region as approximately an ideal spring. The bottom of the interatomic potential is approximately parabolic like the potential energy curve of an ideal spring. If you don't remember this, review Figure 4.3.2.
Elastic Moduli of Common Engineering Metals
This table shows elastic moduli, shear modulus (analogous to modulus of elasticity but under shear instead of tension):
| Metal Alloy | Modulus of Elasticity (GPa) | Shear Modulus (GPa) | Density | Price |
|---|---|---|---|---|
| Aluminum | 69 | 25 | $2.70\ce{g/cm^3}$ | 1K USD/mt |
| Brass | 97 | 37 | $8.73\ce{g/cm^3}$ | 3.5K USD/mt |
| Copper | 110 | 46 | $8.93\ce{g/cm^3}$ | 5K USD/mt |
| Magnesium | 45 | 17 | $1.70\ce{g/cm^3}$ | 2K USD/mt |
| Nickel | 207 | 76 | $8.90\ce{g/cm^3}$ | 10K USD/mt |
| Steel | 207 | 83 | $7.60\ce{g/cm^3}$ | 0.2K USD/mt |
| Titanium | 107 | 45 | $4.50\ce{g/cm^3}$ | 6K USD/mt |
| Tungsten | 407 | 160 | $19.25 \ce{g/cm^3}$ | 30K USD/mt |
Poisson's Ratio
As we have seen, when a material is put under tension, it stretches. Most materials will also contract in the perpendicular direction at the same time as illustrated in Figure 11.4.3. The ratio between the how much the material lengthens in the direction of tension vs how much it contracts in one of the perpendicular directions is known as Poisson's Ratio:
Where $\epsilon_z$ is the tensile strain in the direction of tension and $\epsilon_x$ and $\epsilon_y$ are the tensile strains in the two perpendicular directions.
Poisson's ratio compares how much a material changes shape when under tension compared to how much it changes volume. Using the definition of Poisson's ratio, the following relationship between change in volume and change in length can be derived:
Where $V$ is the original volume of the material and $L$ is the original length. From this expression we can more easily see how Poisson's Ratio relates to shape vs volume change:
- If $\nu=0.5$, then there is no volume change under tension (the right hand of Eq. 11.4.3 is 0 which means the $\Delta V$ must also be zero $\rightarrow$). The material contracts, but at a rate that preserves the volume given the increase in length. Rubber is very close to this with $\nu=0.4999$
- If $\nu$ is 0.2-0.45, there is an increase in volume as the material stretches. Metals behave this way.
- If $\nu=0$, there is no contraction/expansion of the width as the material stretches. Cork behaves this way, which is why it is used plug bottles.
- $\nu<0$ would imply that the material expands laterally when in tension. Such materials, called Auxetic do exist and are discussed next.
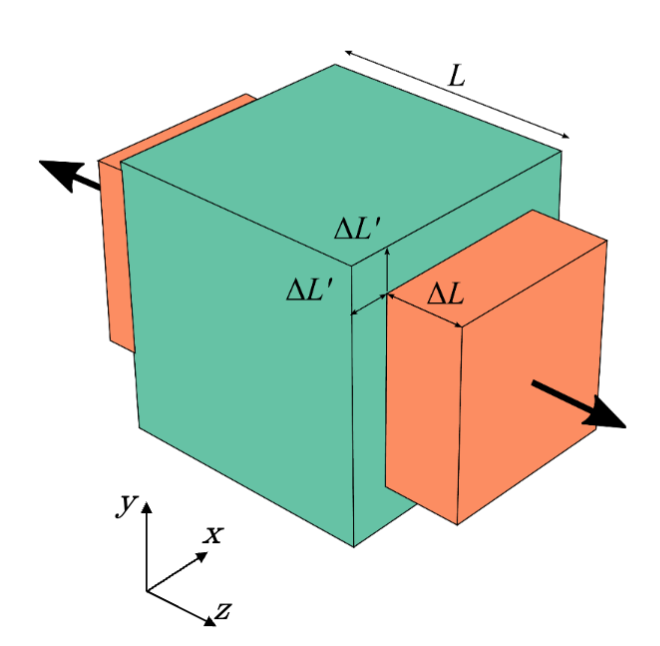
Figure 11.4.3 Illustration of a cube of material being put under tensile strain in the $z$ direction, and as a result contracting in the $x$ and $y$ directions.
Auxetic materials
Auxetics are materials or structures which, when under tension, expand in the perpendicular direction, contrary to most materials. This behavior is the result of particular structures which can be microscopic or macroscopic. One such structure is illustrated in Figure 11.4.4.
Auxetics are used for a number of engineered applications such as for impact resistant materials and smart bandages (which have wound-healing agent in them which is released when the bandage is stretched). A number of biological materials are also auxetic including cat skin, cow udder skin, bovine arteries, human tendons, and stem cells.
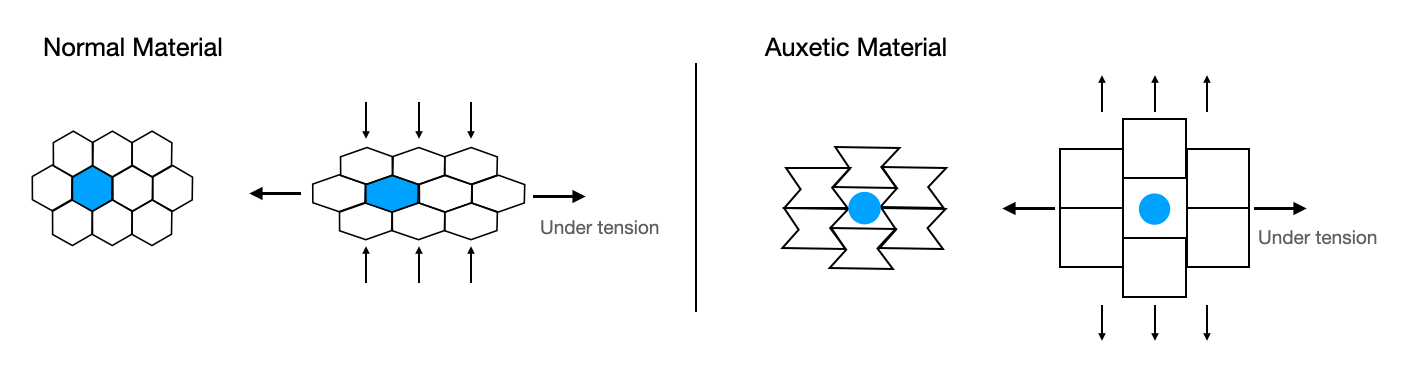
Figure 11.4.4 Left: Normal material contracts in the direction(s) perpendicular to a tensile force. Right: Auxetic materials expand in one or more of the direction(s) perpendicular to the tensile force.