Inelastic Properties

Section 11.4 discussed elastic properties, including Young's Modulus which can be derived from the slope of the initial linear portion of a stress-strain curve. This page focuses on inelastic properties which can be derived from the next region of the stress-strain curve where plastic (i.e., permanent) deformation occurs. These mechanical properties are crucial to consider when choosing a material for an application.

Figure 11.5.1 shows an animation of plastic deformation occurring under tension of a microscopic material made of a small number of atoms. As can be seen there, plastic deformation at a microscopic level corresponds to bonds breaking and then new bonds forming. When the stress is removed, the material will not go back to its original shape. In macroscopic materials, the mechanisms for bonds breaking is more complicated than what is shown in Figure 11.5.1. This will be discussed in Chapter 12.

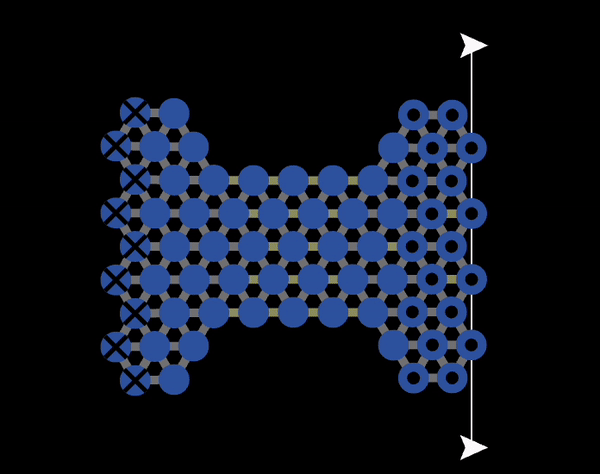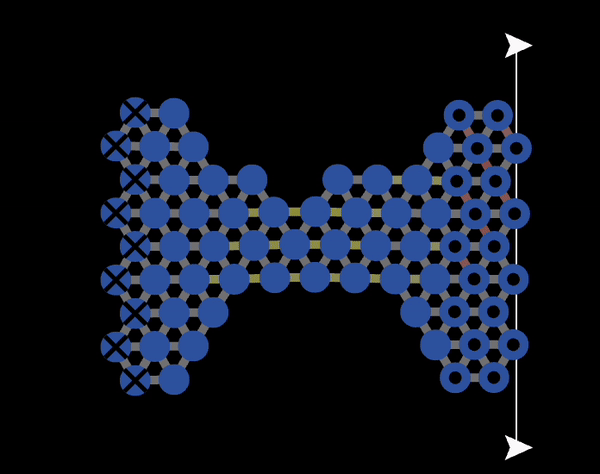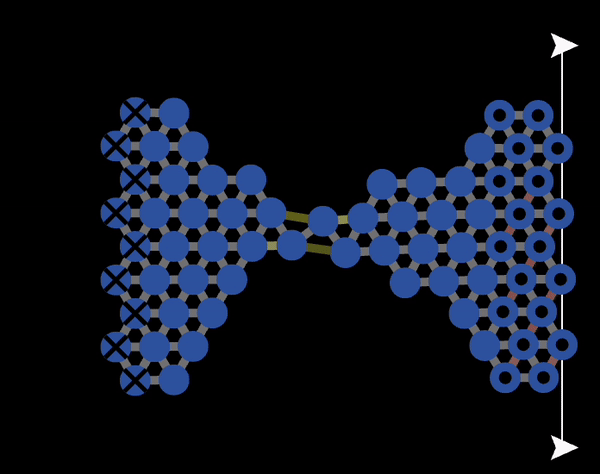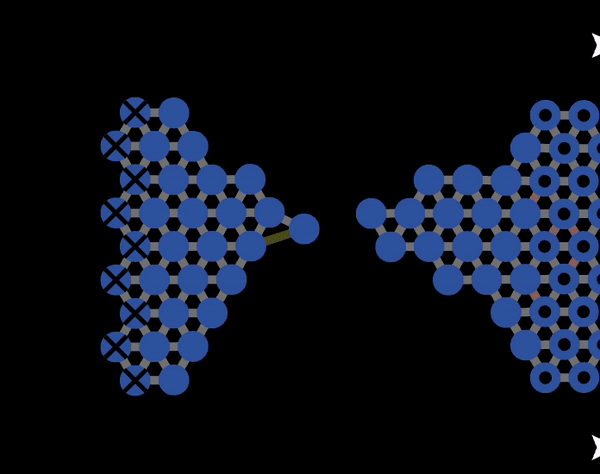
An animation of plastic deformation and breaking produced with @ref(CB10855)

Figure 11.5.1 An animation of plastic deformation and breaking produced with NetLogo model 11.3.1

Yield Strength

Yield strength or yield stress, $\sigma_y$, refers to the stress required to initiate plastic deformation. This is an extremely important property because most designed structures and components are intended to maintain their shape. So, it is important to ensure that the stresses that a material will undergo will be less than $\sigma_y$.

On a stress-strain curve for metals, plastic deformation occurs when the linear-elastic region ends. This point is called the proportionality limit, because afterwards, stress and strain stop being proportional to each other. It is indicated with a $P$ on Figure 11.5.2. However, it is difficult to determine exactly where this point is. For this reason, there is a convention to draw a straight line parallel to the linear portion of the stress-strain curve at a specified strain, usually 0.002, as shown in Figure 11.5.2. Where this line intersects the stress-strain curve is defined as the yield strength, $\sigma_y$ with units of MPa or psi.

Yield strengths of aluminum alloys range from around 10-50Mpa. Low strength steels typically have a yield strength of 200-300 MPa, while high-strength alloy steels can have a yield strength exceeding 1500Mpa.

$Yield strength using the 0.002 offset method. $P$, the proportionality limit, is where plastic deformation being microscopically, but since it is difficult to measure, a line is drawn parallel to the linear region of the stress-strain curve starting at a strain of 0.002 and where it intersects the stress-strain curve is defined as the yield strength $\sigma_y$$

Figure 11.5.2 Yield strength using the 0.002 offset method. $P$, the proportionality limit, is where plastic deformation being microscopically, but since it is difficult to measure, a line is drawn parallel to the linear region of the stress-strain curve starting at a strain of 0.002 and where it intersects the stress-strain curve is defined as the yield strength $\sigma_y$

(Ultimate) Tensile Strength

Tensile strength refers to the maximum tension you can apply to a material before it will break. Until the proportionality limit, P, the stress needed to strain a material follows Hooke's Law, i.e., they are proportional. After yielding, the stress needed to further strain the material continues to increase sublinearly up to the tensile strength (MPa or psi), which is the maximum on the stress strain curve, as shown in Figure 11.5.3. The reason for this continued increase will be explained in Chapter 12. It is worth considering why the microscopic changes depicted in Figure 11.5.1 would not be able to account for this phenomenon. For any applied stress greater than P but less than the tensile strength, some plastic deformation will occur but the material will stop deforming. If stress is increased beyond the tensile strength, the material will break.

Figure 11.5.3 A typical stress-strain curve of a metal.

Ductility

Ductility is a measure of how much plastic deformation can occur before fracture. A material that deforms very little is known as brittle and those that deform a lot before fracture are ductile. Typically, metals with a fracture strain less than about 5% are considered brittle. It is often important to know how much a material will deform before fracture, including because this determines how much deformation is allowable during fabrication and manufacturing processes.

Ductility can be quantified either as the percent elongation, $\%EL$, or by percent reduction in area, $\%RA$. Percent elongation is the percentage of strain when fracture occurs:

$$\%EL=\frac{l_f-l_0}{l_0}\times100 \tag{11.5.1}$$

where $l_f$ is the final length of the material and $l_0$ is the original length. Since $\%EL$ is expressed as a percentage, it will not depend on the specific size of the material tested.

Similarly, percent reduction in area is defined as the percent difference between the original cross-sectional area, $A_0$ and the final cross-sectional area, $A_f$:

$$\%RA=\frac{A_0-A_f}{A_0}\times100 \tag{11.5.2}$$

Resilience

Resilience refers to how much energy a material can absorb and store from elastic deformation and release it again after unloading. This is quantified with the modulus of resilience, $U_r$, which corresponds to the area under the stress-strain curve up until the yield stress, as shown in the shaded region of Figure 11.5.4. This is an elastic property, but it is introduced on this page because the concepts of yield strength and strain are required to define it. Mathematically modulus of resilience is defined as:

$$U_r=\int_0^{\epsilon_y}\sigma d\epsilon \tag{11.5.3}$$

If we assume a linear elastic region, we get:

$$U_r=\frac{1}{2}\sigma_y \epsilon_y \tag{11.5.4}$$

Figure 11.5.4 Representation of how modulus of resilience (shaded area) is determined from a stress-strain curve.

Units of Resilience

Resilience is a measure of energy absorption, but it is normalized to the volume of material since it is product of stress (which is force divided by the cross sectional area of the material) and strain (which is elongation divided by the original length of the material) (see Section 11.3.2). Multiplying these out results in work (energy) divided by volume:

$$\sigma \cdot \epsilon = \frac{F}{A_0}\cdot \frac{d}{l_0}=\frac{W}{V_0}$$

the SI unites of which are $\pu{J/m^3}$, energy per unit volume.

This makes sense. If you take two metal rods of the same length but one is thicker (has a larger cross-sectional area), it will take more force to strain the thicker one and therefore it will absorb more energy. Similarly, with two metal rods of the same thickness but different lengths, it will take more energy to strain the longer one by a given strain. But, since the modulus resilience is divided by unit volume of a material, it is an intrinsic property of the material that doesn't depend on the shape of the material.

(Tensile) Toughness

Toughness of a material refers to how much total energy it takes to deform a material. In the case of a tensile test this is the area under the stress-strain curve until fracture. Unsurprisingly, it has the same units as the coefficient of resilience discussed above. Figure 11.5.5 depicts the toughness of a brittle and ductile material. Even though the brittle material has a larger Young's Modulus and yield stress, it has a lower toughness since it fractures under less strain.

There are other measures of toughness as well, such as the amount of energy needed to deform a material under a high strain rate. The amount of energy it takes to deform a material when it is impacted by a quickly in a small area might be very different from the low strain rate situation of a tensile test in which force is increased slowly.

$Stress-strain curves for a brittle and ductile material. The areas under the curves before fracture correspond to the tensile toughness of the materials.$

Figure 11.5.5 Stress-strain curves for a brittle and ductile material. The areas under the curves before fracture correspond to the tensile toughness of the materials.

Exercise 11.5.1: Information from a Stress-Strain Curve

Not Currently Assigned

Select all that Apply: Which of the follow properties cannot be derived from the stress-strain curve shown in Figure 11.5.6? Explain.

Note, the linear-elastic region is inset in the middle of the graph:

Poisson's Ratio
Yield Strength
Ultimate Tensile Strength
Young's Modulus
Resilience
Shear Modulus
Elongation-to-fracture (ductility)

Figure 11.5.6 A generic stress-strain curve.

Stress-strain Curves

Watch the video below and complete Exercise 11.5.2.

Exercise 11.5.2: Deriving Material Properties from Stress-strain Curves

Not Currently Assigned

Using Figure 11.5.6 estimate Young's modulus.

Using Figure 11.5.6, estimate the Yield strength, $\sigma_y$, using the 0.002 offset method.

Using Figure 11.5.6, estimate the ultimate tensile strength.

Using Figure 11.5.6, estimate the elongation-to-fraction (ductility).

Using Figure 11.5.6, estimate the modulus of resilience (use reasonable approximations).

Using Figure 11.5.6, estimate the tensile toughness (use reasonable approximations).