Metal vs Insulator Conduction? Why?
On this page, we will introduce two related models to answer the question: why do some materials conduct electricity and some don't? These two related models are complementary. Use whichever one is easier for you to think with, or both.
Before introducing them, we need to introduce resonance structures, fractional bonds, and delocalized electrons.
Resonance Structure, Fractional Bonds, and Electron Delocalization
When we consider the bonding of atoms, sometimes there are multiple equivalent configurations represented by Lewis structures. For example ozone, $\ce{O}_3$, could be represented as having a double bond on either side as shown in Figure 13.6.1 below. Oxygen has six valence electrons, allowing for three bonds between the three atoms.

Figure 13.6.1 Resonance structures of ozone.
Based on these structures, it would seem that the ozone molecule should have one single bond and one double bond, which would have different lengths. It turns out, that the two bonds in ozone are identical. So, what is going on?
As discussed on Section 3.5, the behavior of electrons in atoms cannot be understood as particles with a single position. We have to describe them as spread out in "probability clouds" that are at least somewhat spread out in space. In the case of the ozone molecule, we can think of the double bond as spread out across the two equivalent possibilities. In the language chemists use, the molecule is said to resonate between the two structures in Figure 13.6.1 which are then called resonance structures.
Another way of depicting the ozone molecule is shown in Figure 13.6.2 with two one-and-a-half bonds instead of a single bond and a double bond. These are known as fractional bonds. Keep in mind, that both descriptions of the ozone molecule as (a) resonating between the two structures in Figure 13.6.1 or as (b) simultaneously having two fractional bonds are both models of the real molecule. They are useful representations, but not the "whole truth" as discussed on Section 2.5. In either case, we describe the electrons as delocalized. For our purposes, an electron is delocalized if it participates in bonding between more than two atoms.
For a short and insightful discussion of the history of resonance theory and the idea of fractional bonds, you can read Linus Pauling's 1954 Nobel Prize Lecture.

Figure 13.6.2 Ozone molecule depicted with two fractional 1.5 bonds.
Resonance perspective on why metals conduct electricity
The model introduced here originates with Linus Pauling (see his discussion here). We will introduce the model from two complementary perspectives: Pauling's bottom-up perspective and then from a more empirical top-down perspective.
Pauling uses Lithium as the example conductor due to its simplicity and the following discussion is based on his paper. Lithium is the third element in the periodic table. It is in the same group (column) as hydrogen and has one valence electron. If you imagine bringing together four Lithium atoms in a square crystal and assume they each have only one bond, they could be bonded as shown below on the left of Figure 13.6.3. Given these configurations are equivalent, the crystal will have lower energy if the bonds resonate between these positions. But, Pauling argues, the crystal will be even more stable if bonds can also resonate in other configurations resulting in momentary unbalanced charges of the lithium ions as sown on the right of Figure 13.6.3.

Figure 13.6.3 On the left, bonds only resonate in ways that maintain charge balance on the lithium atoms which Pauling calls "synchronized resonance". On the right, charge balance is broken, in an "unsynchronized resonance" structure leading to some positive and negative lithium ions in the crystal.
Since the electrons in the lithium crystal are resonating between these different bond states, they are free to move around. If a voltage is applied a lithium crystal as shown in in Figure 13.6.4, then the electrons will move towards the anode, resulting in conduction of electricity.

Figure 13.6.4 Animation of an electron moving from cathode to anode in a lithium crystal due to successive "pivoting" resonances of bonding electrons.
Fractional bond perspective on why metals conduct electricity
We present a related but different model that starts from different assumptions but reaches the same conclusion. Pauling imagines a hypothetical scenario of bringing together four lithium atoms into a crystal. We could instead start from the empirical fact that lithium forms a BCC crystal, meaning each atom has 8 nearest neighbors, yet we know that it has only one valence electron. Using the perspective of fractional bonds, this means that each bond must be a $\frac{1}{8}$ fractional bond, as shown in Figure 13.6.5 below.

Figure 13.6.5 Lithium forms a BCC structure with 8 nearest neighbors. In each close-packed plane, there are four nearest neighbors each with a fractional $\frac{1}{8}$ bond.
These fractional bonds implies the electrons are delocalized around the lithium ionic cores - aligning with the models we introduced in Chapter 3. If a voltage is applied across the crystal as shown in Figure 13.6.6 , the delocalized electron cloud around each ionic core is largerly free to shift from away from the cathode and towards the anode, i.e., from the right to left of the ionic core. Notice, however, that there is no way to distinguish these electrons as "belonging" more to the bolded lithium ions than to those lithium on their left. So, the delocalized electrons are free to shift to the left of those atoms as well, and so on, resulting in electrons freely moving across the whole material. This is depicted in an animation in Figure 13.6.7.
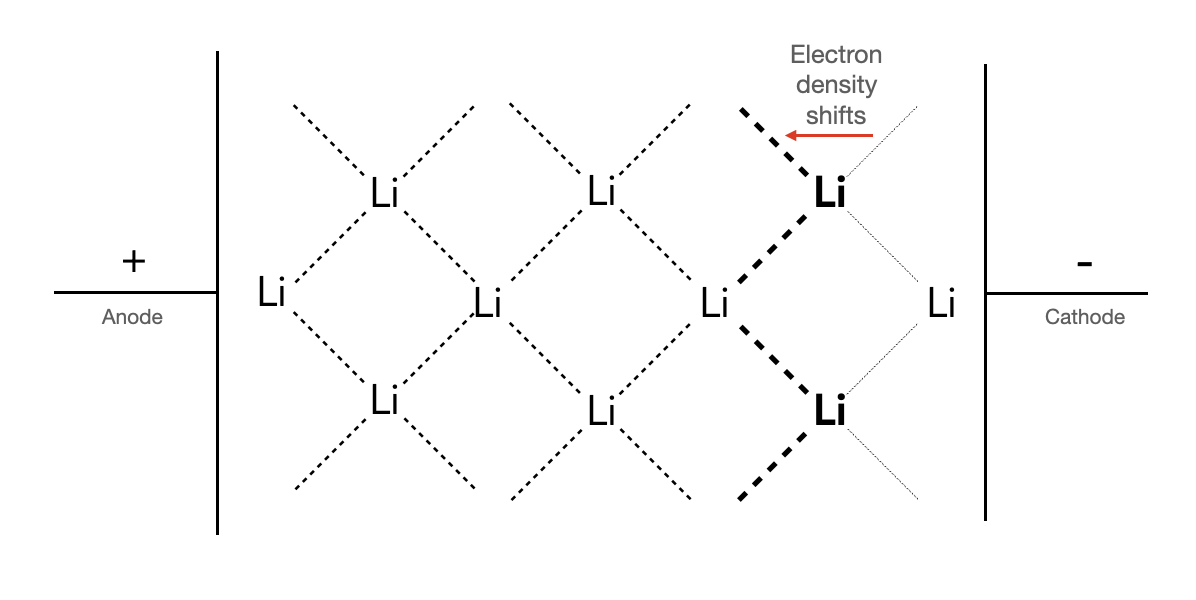
Figure 13.6.6 A depiction of electron density shifting in the close-packed plane of a BCC lithium crystal due to an applied voltage. In the absence of a voltage, each bond is an equal $\frac{1}{8}$ bond, but the voltage will push the electrons, causing the bond fractions to be unbalanced.

Figure 13.6.7 Animation of current through the close-packed plane of a Li crystal using a fractional bond model.
Why insulators don't conduct electricity
We can use the same models explain why insulators don't conduct electricity. As an exercise, try to answer the question below in Exercise 13.6.1 about why carbon in the diamond structure does not conduct electricity while carbon in the graphene structure does. Both structures are depicted in Figure 13.6.8 below. After you try to explain it, you will be able to see an explanation.

Figure 13.6.8 On the left is the crystal structure of diamond and on the right is the structure of graphene. Both are made of pure carbon. Diamond forms a 3D material in which each carbon atom has 4 neighbors. Graphene is a 2D material in which each carbon atom has 3 neighbors.