Historical Anomalies in Plasticity Theory
The discovery of X-ray diffraction in 1912 allowed scientists to determine the crystal structure of materials. The theory of crystal structure had been established centuries earlier, but scientists were not convinced of these models. Undeniable confirmation that many materials were comprised of regular arrays of crystal lattices came when German physicist Max von Laue acquired a diffraction pattern for a copper sulfate crystal.
In the subsequent decades, many studies of the mechanical properties of metals were conducted. A theoretical model to explain plastic deformation was developed known as the slip model (or glide model). This model proposed that atoms under enough stress slip past each other in the close packed direction resulting in plastic deformation. This is what we observed with NetLogo model 11.3.1 and is also illustrated below in Figure 12.3.1. In this animation, you can observe that when bonds break, atoms slip past each other into a new configuration.
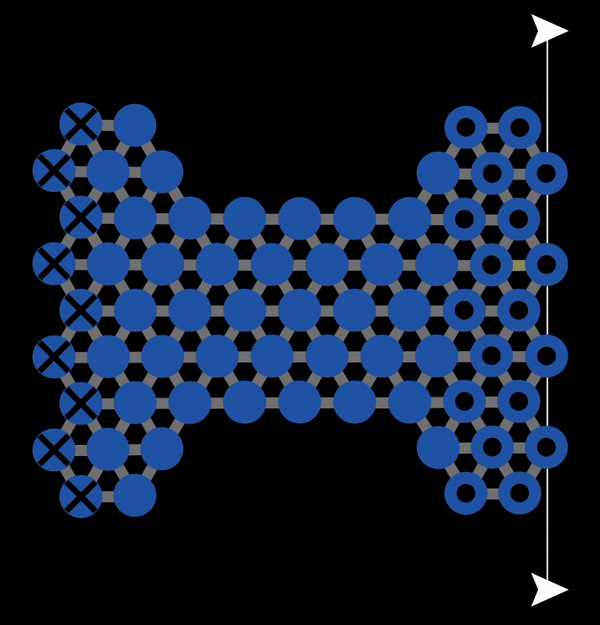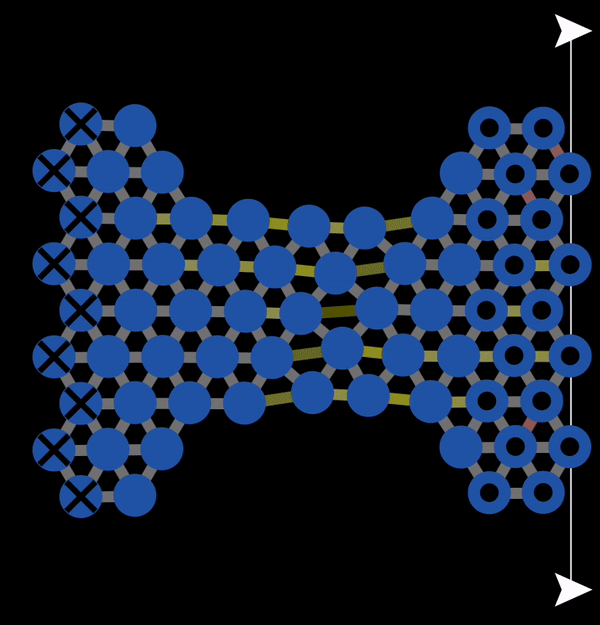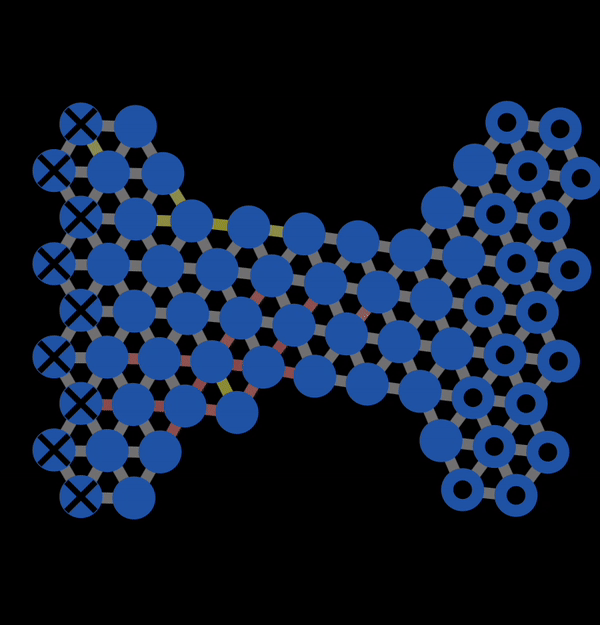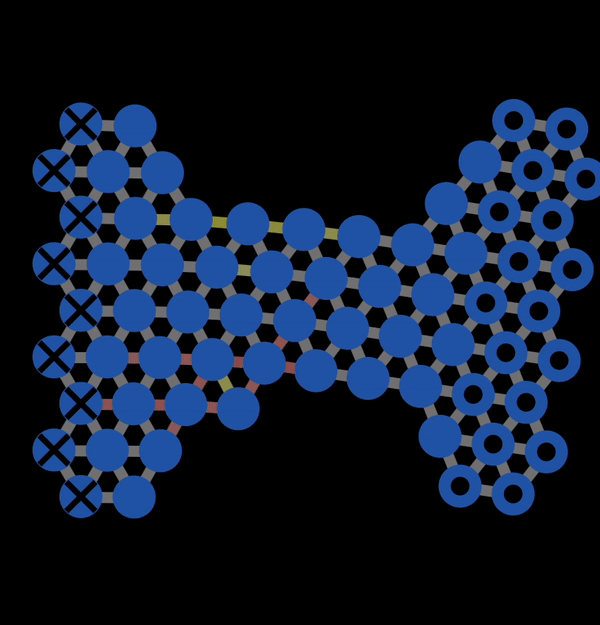
Figure 12.3.1 A Gif created with NetLogo model 11.3.1 of slip occurring under tension resulting in permanent (plastic) deformation.
However, the slip model ran into a number of difficulties that it could not explain. It implies that if you know the strength of bonds in a crystal, then you can calculate what the expected strength of the material (i.e., the force needed to induce slip) by calculating the approximate number of bonds in the cross-section of the material and multiplying by the strength of a bond. However, the experimentally measured strengths of metals turned out to be two to three order of magnitude lower than the theoretically predicted values.
In the table below are the predicted values of the shear strength needed to cause plastic deformation for some metals predicted by the slip model. The table compares these theoretical values to the experimental ones.
| Material | $\tau_\text{theory}[10^6\ce{N/m^2}]$ | $\tau_\text{experiment}[10^6\ce{N/m^2}]$ |
|---|---|---|
| Ag | $1.0 \times 10^3$ | $0.37$ |
| Al | $0.9 \times 10^3$ | $0.78$ |
| Cu | $1.4 \times 10^3$ | $0.49$ |
| Ni | $2.6 \times 10^3$ | $3.20$ |
| $\alpha$-Fe | $2.6 \times 10^3$ | $27.5$ |
The disagreement perplexed physicists (this was before "materials science" was a thing: all materials scientists were physicists or chemists). It also stymied technological development of metals at the time - if we did not have a good model for understanding plasticity, how could we intentionally design better metals?
Let's further consider this puzzle. Complete Question 12.3.1.1.