Dislocations
The very low yield strength of metals compared to what would be predicted in a perfect crystal led scientists to realize that there must be defects of some kind. A perfect crystal with atomic planes simply slipping past each other could not account for the experimental results. However, an imperfect crystal did not require all bonds to break along a slip plane at the same time, and could explain these anomalies.
In 1934, Taylor, Polyani, and Orowan independently proposed the idea of dislocations to explain the plastic properties of crystals. In contrast to point defects, which exist at points within a lattice, dislocations are line defects that extend along lines in a crystal.
The simplest dislocation to visualize is as an edge dislocation, which is shown in 3D projection and in a NetLogo model in Figure 1.12.1.
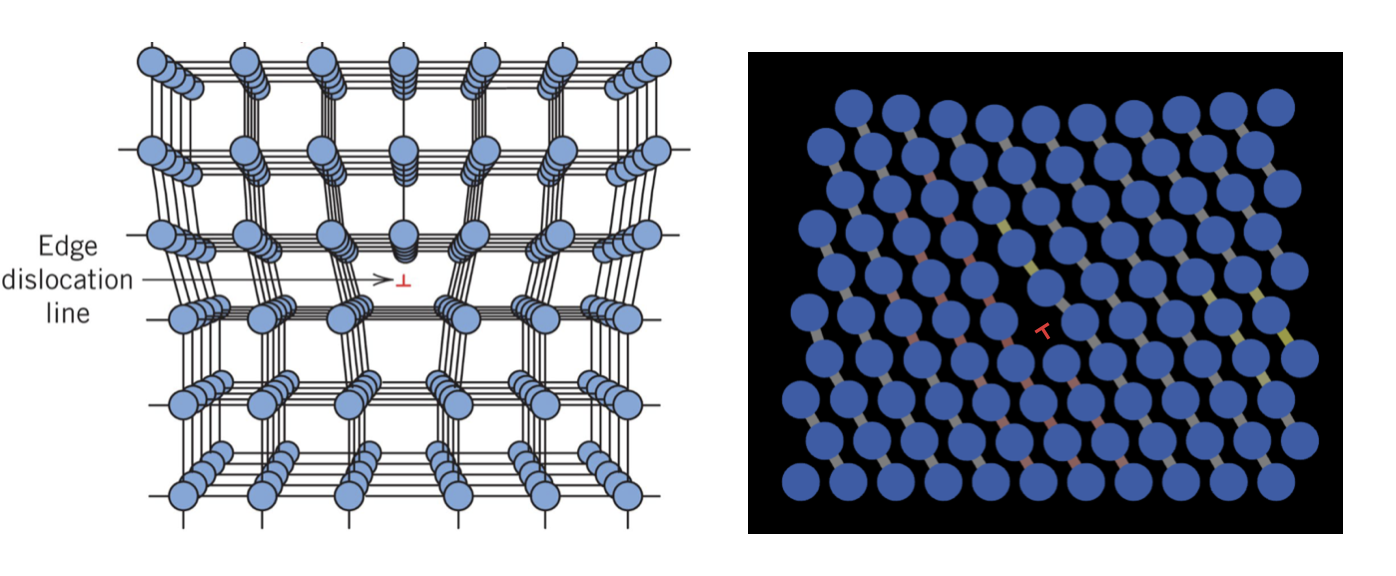
Figure 1.12.1 Two illustrations of edge dislocations. Left: an edge dislocation in a 3D cubic lattice. Right: an edge dislocation in a 2D hexagonal lattice created with NetLogo model 1.12.1 below.
Let's investigate what's going on a bit more closely, because this can be a bit difficult to visualize. In Figure 1.12.1 we see a crystal (a simple cubic one, in this case), but at the center of the model (indicated by a red $\bot$ symbol) there is a region that looks defected. Some of the atoms there have low coordination, and other atoms may have their interatomic bonds stretched or compressed. This defect runs into the crystal from your view. There is essentially a line of atoms with non-ideal coordination. Because these defects of a linear topology (as opposed to point defects, for example), we call it... well, a line defect.
Another way to visualize this is that you had a perfect crystal but you shoved an extra half-plane of atoms into the bulk, terminating at the center of the crystal. Since this plane possesses an "edge" in the crystal itself and dislocates (or moves) other atoms out of their equilibrium positions, we call this defect an edge dislocation. However, it is important to notice that far away from the dislocation the crystal is essentially perfect. So, like point defects, the disruption in the crystal lattice is local, usually only disrupting the crystal to maybe 5$r_0$, where $r_0$ is the interatomic bond distance.
There are some other types of dislocations, which we'll show, but we'll focus on this edge dislocations.
Motion of a Dislocation
A classic analogy can help make sense of dislocation motion: Goldie the Caterpiller (Figure 1.12.2, credit to Charles Frank, University of Bristol). Goldie's caterpillar feet are all stuck the the ground. If you try to viciously grab Goldie and move all of her feet at once (left), you can do it, but it's going to take quite a bit of force (and make Goldie mad) to move her one unit to the right.
However, if you instead sneak up behind Goldie and give her a swift kick, you can break a single bond between the caterpillar and the ground, that's not so hard - it is just one bond. Then, perhaps with a bit more pushing, Goldie will to a "Caterpillar Roll", displacing each leg in sequence until she has moved by one unit. This takes much less force and Goldie is happy afterwards, although perhaps a bit surprised with the kick.
In a crystal, instead of legs attached to the ground, we have atomic bonds. The bonds will only break along the dislocation line, not the entire plane, enabling the dislocation to "roll" through the crystal. In small systems, like that modeled in NetLogo model 1.12.1, there is enough strain from the dislocation that it "kicks" itself out without any external force. However, in macroscopic materials, dislocations often get stuck and will only move when an external force is applied.
Another way to imagine this: try pulling a rug across a floor. If you've got a big rug, this is not easy. However, if you create a roll in the rug and pull it, you can instead easily roll it, bit by bit, across the room.
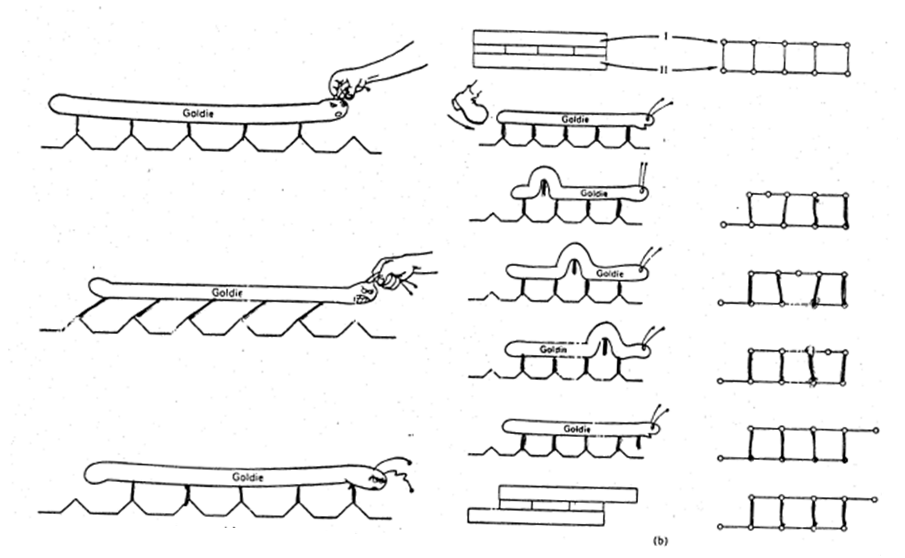
Figure 1.12.2 Goldie the Caterpillar - pulling all her legs off at once is hard! Instead, she "rolls" her body, breaking one bond at a time until she's moved!
A Non-computational Model of Dislocations
The theory of dislocations continued to develop, but direct experimental confirmation of the theory didn't arrive until over two decades later. Video 1.12.1, from 1952, shows a model that scientists made of dislocations out of bubbles! This is a very cool demonstration that models don't have to be computational or mathematical. They can be physical too.
Video 1.12.1